어떤 배열의 특정 범위에 해당하는 수의 합을 구할 때 부분 합을 사용한다.
이 부분 합의 전처리 과정의 시간 복잡도는 O(N)이고 원하는 값을 구할 때의 시간 복잡도는 O(1)이다.
전처리 과정
sum[ i ]의 값을 arr의 인덱스 0부터 인덱스 i 까지의 합이라고 정의하고 아래와 같은 배열이 있다고 하자.

sum[0]은 1일 것이고 sum[1]은 9일 것이고 sum[2]는 12일 것이다.
이를 구하는 과정을 파이썬을 나타내면 다음과 같고 시간 복잡도는 O(N)이다.
arr=[1, 8, 3, 4, 6, 7, 4, 4]
sum=[0 for _ in range(8)]
sum[0]=arr[0]
for i in range(1, 8):
sum[i]=sum[i-1]+arr[i]원하는 값 구하기
그런데 위 sum 배열은 누적 합이지 부분 합이 아니다. 인덱스 2부터 5까지의 합을 미리 구해놓지는 않았다.
그러나 인덱스 2부터 5까지의 부분 합은 sum[5] - sum[1]과 같이 구해놓은 누적 합의 뺄셈을 통해 구할 수가 있고 이는 상수 시간 안에 구할 수 있다.
그런데 만약 여기에 갱신 연산이 추가되면 어떨까?
특정 인덱스의 값을 원하는 수로 바꾸는 연산이 추가된다면 상당히 복잡해진다.
만약 위 arr 배열에서 arr[1]의 값을 바꾼다면 sum[1]부터 sum[7]까지의 모든 값을 바꿔야 한다.
즉 갱신 연산의 시간 복잡도가 O(N)이 되는 것이다.
| 전처리 | 값 구하기 | 수정 |
| O(N) | O(1) | O(N) |
그래서 이제 갱신 연산이 추가된 부분 합을 구할 때의 자료 구조를 알아보려고 한다.
갱신 연산이 포함된 부분 합
두가지 방법에 대해서 알아보려고 한다.
첫 번째 방법은 루트 N가지의 블록으로 배열을 나누는 것이다.
길이가 9인 배열이 있다고 하면 길이가 3인 배열 3개로 나누는 것이다.

이 상태에서 arr[2]부터 arr[7]까지의 부분합을 구하고 싶다면 먼저 arr[3]부터 arr[5]까지는 미리 구해놓았기 때문에 바로 구할 수가 있다.
이를 구하고 나서 arr[1]과 arr[6], arr[7]은 따로 더해주면 된다.
만약 arr[3]을 수정하려고 한다면 해당 블록(arr[3], arr[4], arr[5])의 값에서 arr[3]을 빼서 수정된 값을 더해주면 된다.
시간 복잡도는 다음과 같다.
| 전처리 | 값 구하기 | 수정 |
| O(N) | O(sqrt(N)) | O(1) |
두 번째 방법은 BIT를 사용하는 방법이다.
BIT (Binary Indexed Tree, 펜윅 트리)
이진 인덱스 트리, 펜윅 트리라고도 불리는 BIT에 대한 설명은 백준을 참고했다.
https://www.acmicpc.net/blog/view/21
펜윅 트리 (바이너리 인덱스 트리)
블로그: 세그먼트 트리 (Segment Tree) 에서 풀어본 문제를 Fenwick Tree를 이용해서 풀어보겠습니다. Fenwick Tree는 Binary Indexed Tree라고도 하며, 줄여서 BIT라고 합니다. Fenwick Tree를 구현하려면, 어떤 수 X
www.acmicpc.net
이진 인덱스 트리라고도 불리는 BIT를 이해하기 위해서는 RSB(rightmost set bit)에 대해서 알아야 한다.
RSB는 이진수에서 가장 오른쪽에 있는 값이 1인 비트의 위치이다.
예를 들어서 14라는 숫자가 있다고 하면 이진수로 나타내면 1110이다.
여기서 RSB는 빨간색이다.
1110
오른쪽부터 2번째에 위치하기 때문에 14의 RSB는 2이다.
12를 보면 1100이고 12의 RSB는 3이 된다.
1100
우리는 이 2^(RSB-1)의 값을 "범위"로 사용할 예정이다.
2^(RSB-1)의 값이 감이 잘 안 잡힐 수 있는데 위에서 빨간색으로 표시한 비트 외에는 모두 0으로 바꾼 값이다.
즉 14의 rsb는 2이고 빨간색 비트를 제외하고 모두 0으로 만들면 0010, 즉 2이고 이는 2^(2-1)의 값이 된다.
이 값을 구하는 간단한 방법이 존재한다. 바로 논리 연산자인 &연산자를 사용하는 것이다.
6을 예시로 들어보자.
6은 이진수로 나타내면 0110이다.
여기서 모든 비트를 반전시키면 1001이 된다.
이 반전시킨 값에 1을 더해보면 1010이 된다.
&연산자는 두 비트 모두가 1인 경우만 1이고 나머지 경우는 모두 0이다.
0110과 1010에 &연산자를 적용한다면 0010이 나온다.
그리고 어떤 수 n이 있을 때 n의 모든 비트를 반전한 후 1을 더하면 -n이 된다.
이를 활용하여 n&-n 연산을 사용하면 가장 오른쪽에 있는 값이 1인 비트를 제외하고 모든 비트가 0인 값을 구할 수 있다.
이제 tree[n]를 정의해보자.
tree[n]의 값은 arr[n] 값부터 arr[n - 2 ^ (RSB (n) - 1) + 1]값 까지의 부분 합이다.
그림으로 보는 편이 더욱 이해하기 쉬울 것이다.
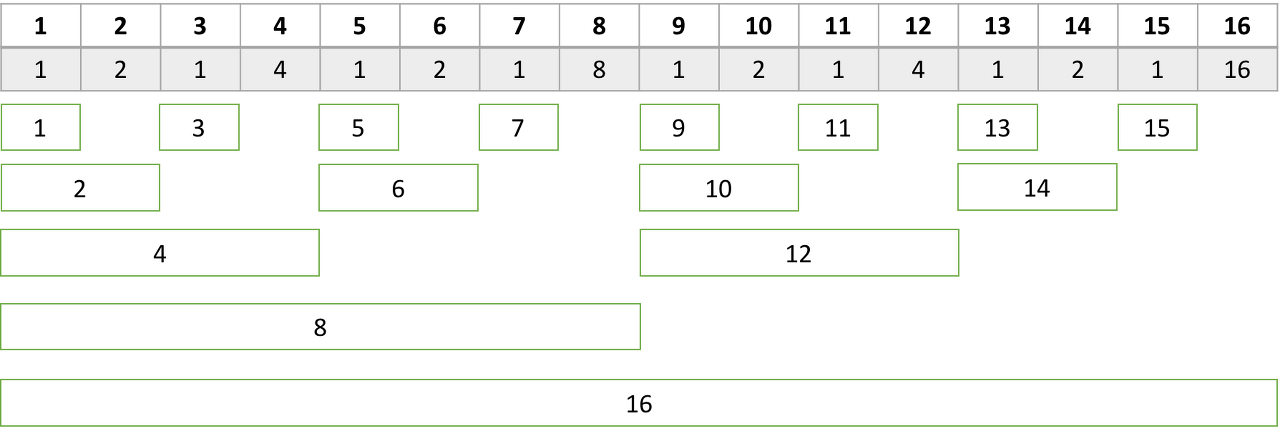
초록색 블록들은 "범위"를 의미한다.
tree[1]는 부분 합으로 그에 해당하는 범위는 초록색 블록이다.
위 그림을 바탕으로 다시 한번 이해해보자.
tree[12]를 구하고 싶다면 어떻게 할까?
우선 2^( RSB(12) - 1 )를 구한다. 1100에서 가장 오른쪽 값이 1인 비트를 제외하고는 전부 0으로 만든다.
0100의 값은 4가 되고 2^( RSB(12) - 1)의 값이 4가 된다.
즉 tree[12]의 값은 arr[12]부터 arr[12 - 4 +1]까지의 부분 합이 되는 것이다.
이제 이 범위를 바탕으로 값을 모두 구한다면 다음과 같다.

이제 여기서 누적 합을 구하는 방법은 다음과 같다.
A[11]까지의 누적 합을 구하고 싶다면 다음처럼 색칠되어있는 부분을 더하면 된다.
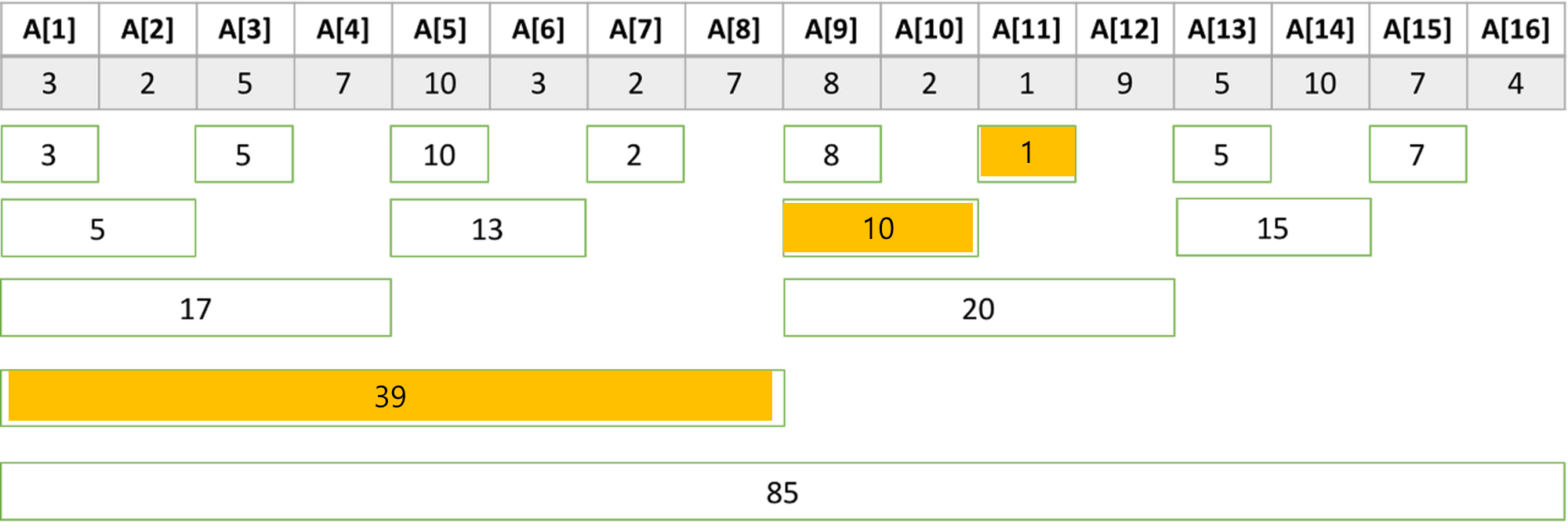
또한 A[3]의 값을 바꾸고 싶다면 이 값을 가지고 있는 블록들의 값만 바꾸면 된다.
시간 복잡도는 다음과 같다. (M은 연산의 개수, N은 배열의 길이)
| 전처리 | 값 구하기 | 수정 |
| O(M * log N) | O(log N) | O(log N) |
'공부 > Algorithm' 카테고리의 다른 글
| [Algorithm] 컨벡스 헐 만들기(Convex Hull), Graham Scan (0) | 2023.06.02 |
|---|---|
| [Algorithm][백준 11758][파이썬] CCW 알고리즘을 활용하여 선분의 교차 여부 판단 (0) | 2023.04.24 |
| [Algorithm] RMQ (Range Minimum Query) (0) | 2023.04.19 |
| [Algorithm] 다익스트라 (Dijkstra algorithm), 벨만 포드(Bellman ford algorithm) (0) | 2022.12.19 |
| [Algorithm] KMP 알고리즘 (문자열 매칭 알고리즘) (0) | 2022.12.18 |