최적의 경로를 찾는 대표적인 라우팅 알고리즘 두 가지를 알아보려고 한다.
1. link state (Dijkstra's Algorithm)
link state 알고리즘은 다익스트라 알고리즘을 사용한다.
다익스트라 알고리즘은 음의 가중치를 허용하지 않으며 목적지 노드까지의 최단 경로를 구할 때 사용한다.
이를 사용하려면 모든 link의 state를 알아야 해서 link state broadcasting 방식으로 값이 바뀌거나 하면 모든 노드에게 값을 알려준다.
즉 모든 라우터의 정보를 알아야 한다.
이 다익스트라 알고리즘을 사용하면 특정 노드에서 다른 모든 노드로 가는 최단 경로를 알 수 있다.
<다익스트라 알고리즘 참고>
https://growth-coder.tistory.com/41
[Algorithm] 다익스트라 (Dijkstra algorithm), 벨만 포드(Bellman ford algorithm)
그래프에서 특정 노드에서 특정 노드까지 가는 최단 거리를 구하는 알고리즘에 대해서 공부해보려 한다. 다익스트라 알고리즘과 벨만 포드 알고리즘이 있는데 이 둘의 차이는 그래프의 가중치
growth-coder.tistory.com
다익스트라 알고리즘을 사용해서 특정 노드에서 다른 모든 노드까지의 최단 경로를 알아냈다면 forwarding table을 만들 수가 있다.
패킷이 라우터의 입구로 들어오면 가장 적절한 출구로 내보내는 것이 forwarding이다.
또한 다익스트라 알고리즘을 사용한다면 특정 노드에서 다른 모든 노드까지의 최단 경로를 알 수 있다.
위 링크를 보면 알겠지만 A에서 F까지 가는 최단 경로를 구할 때 나머지 노드들에 대한 최단 경로들도 같이 구한다.

즉 A-F의 최단 경로 뿐만 아니라 A-B, A-C, A-D, A-E의 최단 경로 또한 같이 구하는 것이다.
그렇다면 라우터는 어떻게 출구를 알 수 있을까?
최단 경로를 따라가면 된다.
예를 들어 A에 들어온 패킷이 F로 가고 싶다고 하자.
다익스트라 알고리즘을 사용하면 다음과 같은 최단 경로가 나올 것이다.

다익스트라 알고리즘은 재귀적인 방식을 사용하기 때문에 해당 경로의 각 노드에도 F에 도달하기 위한 최단 경로가 기록되어 있다.
A에서 F로 가기위한 경로에서 패킷은 D를 거쳐야 한다.
A에서 D로 가기 위한 경로에서 패킷은 C를 거쳐야 한다.
A와 C는 연결되어 있으므로 F로 가려는 패킷이 A에 들어오면 라우터는 C로 forwarding 하는 것이다.
A의 forwarding table에는 "F 가려는 패킷(input)이 들어오면 C(output)으로 보낸다"와 같은 내용이 적혀있는 것이다.
당연하게도 E로 가려는 패킷이 A에 들어오면 나가는 출구 또한 같은 방식으로 구할 수 있다.
이를 반복하여 A의 forwarding table을 완성하는 것이다.
최단경로
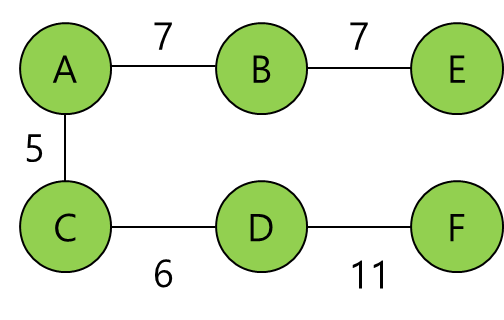
A 라우터의 forwarding table

2. Distance Vecotr Algorithm (Bellman-Ford Algorithm)
link state 알고리즘의 경우 모든 링크의 cost를 알고 사용하는 알고리즘이다.
그에 비해 distance vector 알고리즘은 모든 라우터의 정보를 사용하는 것이 아닌 인접 라우터들의 정보를 사용한다.
A에서 F로 갈 때 중간 노드이면서 A의 이웃 노드인 X를 거친다고 하자.
이 때 A는 A-X 링크의 cost와 X에서 F로 갈 때의 cost를 더한 값들 중에서 가장 작은 값을 선택하는 것이다.
노드 A 입장에서는 A-X 링크의 cost는 자신이 알고 있고 X에서 F로 갈 때의 cost는 자신이 모르기 때문에 X 노드에게 물어보는 것이다.
그래서 link state와 달리 모든 라우터의 정보를 알 필요가 없다.
아래에서 A에서 F까지 가는 최단 경로를 구하려고 한다고 하자.

우선 A의 인접 노드는 B와 C가 있다.
B부터 계산하면
우선 A-B link cost는 A가 알고 있다.(7) 그리고 B에서 F까지의 최단 경로를 물어본다.(B가 F까지의 최단 경로를 이미 알고 있다고 가정한다)
7+16=23이다.
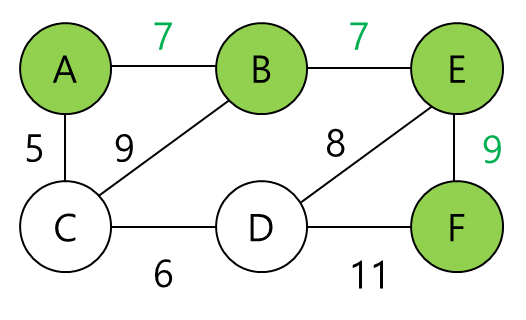
이제 C를 계산하면
우선 A-C link cost는 A가 알고 있다.(5) 그리고 C에서 F까지의 최단 경로를 물어본다.(C가 F까지의 최단 경로를 이미 알고 있다고 가정한다)
5+17=22이다.
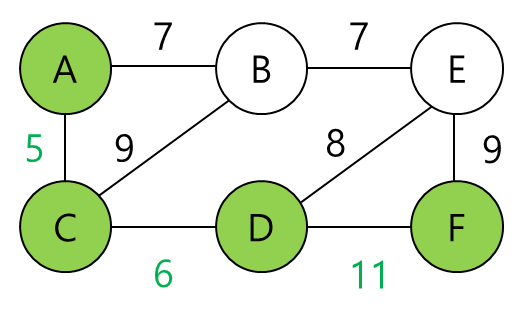
22, 23 중 작은 값은 22이기 때문에 F로 향하는 패킷이 A에 들어오면 B로 보내는 것이 최적의 방법이라고 판단하고 forwarding table에 추가한다.
즉 link state처럼 모든 정보를 가지고 계산하는게 아니라 인접 라우터들의 정보만 가지고 최젹 경로를 판단하는 방법이다.
이 방법은 link cost가 수정될 때 문제가 생길 수 있다.
다음과 같은 link cost들이 있다고 하자.

우선 B 입장에서 A로 가기 위한 최단 경로는 B-C-A이고 cost는 5일 것이다.
그런데 이 상황에서 A-C 링크의 cost가 60으로 바뀌면 어떨까?

C에서 A로 가는 최단 경로를 갱신할 때 문제가 발생한다.
우선 C는 인접 노드인 A와 B의 cost를 가지고 있다.
A의 경우 인접 노드이자 목적지이기 때문에 cost를 알고 있고 60으로 변경되었다는 것도 알고 있다.
우선 A-C 경로의 경우 cost가 60이다.
이제 B로 향하는 경로도 살펴봐야 한다.
C-B link cost는 1로 이미 알고 있는 값이고 B에서 A로 향하는 최단 경로는 B에게 물어보게 된다.
그런데 B의 경우 A-C link cost가 4에서 60으로 바뀌었다는 사실을 모른다.
그래서 B-A 경로가 최단 경로라고 생각하는게 아닌 B-C-A (5)의 경로가 최단 경로라고 C에게 알려주는 것이다.
그러면 우리가 원하는 C-B-A (51)이 최단 경로가 되는 것이 아니라 C-B-C-A (6)이 최단 경로가 되는 것이다.
우리가 원하는 값으로 갱신이 되려면 굉장히 많은 반복을 해야 할 것이다.
이를 Count to infinity problem 이라고 한다.
이를 해결하기 위한 방법 중 하나는 Poisoned Reverse이다.
'공부 > Network' 카테고리의 다른 글
| [Network] SDN(Software Defined Networking) (0) | 2023.06.14 |
|---|---|
| [Network] AS, OSPF, BGP (0) | 2023.06.12 |
| [Network] IPv6와 ICMP (0) | 2023.06.08 |
| [Network] DHCP와 NAT (0) | 2023.06.06 |
| [Network] IP addressing (0) | 2023.06.04 |