https://www.acmicpc.net/problem/1238
1238번: 파티
첫째 줄에 N(1 ≤ N ≤ 1,000), M(1 ≤ M ≤ 10,000), X가 공백으로 구분되어 입력된다. 두 번째 줄부터 M+1번째 줄까지 i번째 도로의 시작점, 끝점, 그리고 이 도로를 지나는데 필요한 소요시간 Ti가 들어
www.acmicpc.net

다익스트라 알고리즘을 사용하는 문제이다. (다음 링크 참고)
https://growth-coder.tistory.com/41
[Algorithm] 다익스트라 (Dijkstra algorithm), 벨만 포드(Bellman ford algorithm)
그래프에서 특정 노드에서 특정 노드까지 가는 최단 거리를 구하는 알고리즘에 대해서 공부해보려 한다. 다익스트라 알고리즘과 벨만 포드 알고리즘이 있는데 이 둘의 차이는 그래프의 가중치
growth-coder.tistory.com
위 링크의 내용을 바탕으로 구현을 해보았다.
위에서는 초록색 노드가 최단 거리가 확정된 노드이고 빨간색 노드는 아직 최단 거리가 확정되지 않은 노드이다.
초록색 노드들과 연결되어있는 모든 빨간색 노드들 중 가장 거리가 짧은 노드는 최단 거리가 확정된다.
이러한 성질을 이용하여 최소 힙을 사용하면 구현할 수 있다. (최소 힙은 다음 링크 참조)
https://growth-coder.tistory.com/128
[백준 1927][파이썬] 최소 힙. 파이썬 heapq 모듈 사용법 (우선순위 큐)
https://www.acmicpc.net/problem/1927 1927번: 최소 힙 첫째 줄에 연산의 개수 N(1 ≤ N ≤ 100,000)이 주어진다. 다음 N개의 줄에는 연산에 대한 정보를 나타내는 정수 x가 주어진다. 만약 x가 자연수라면 배열에
growth-coder.tistory.com
우선 기본적인 환경 세팅은 다음과 같다.
import sys
import heapq
input=sys.stdin.readline
MAX=1e9
n, m, x = map(int, input().split())
graph=[[] for _ in range(n+1)] #그래프
for _ in range(m): #거리 넣기
a, b, t = map(int, input().split())
graph[a].append((b, t)) #a에서 b로 가는데 t시간이 걸림우선 입력 값에 따른 기본적인 그래프를 생성하는 코드이다.
그래프는 다음과 같이 배열로 이루어져있다.
[
[], //0번 노드와 연결된 노드
[(2, 4), (3, 2), (4, 7)], //1번 노드와 연결된 노드
[(1, 1), (3, 5)], //2번 노드와 연결된 노드
[(1, 2), (4, 4)], //3번 노드와 연결된 노드
[(2, 3)] //4번 노드와 연결된 노드
]두 번째 행의 첫 번째 열에는 (2, 4)가 연결되어 있는데 이는 1번 노드와 2번 노드는 거리가 4인 링크로 연결되어 있다는 뜻이다.
n은 1부터 시작하기 때문에 0번에는 항상 빈 배열이 들어간다.
이제 본격적으로 다익스트라 알고리즘을 적용할 차례이다.
그 전에 이 문제는 출발지에서 목적지까지 왕복 거리의 최단 거리를 구하는 문제이다.
즉 한 명마다 출발지 -> 목적지 최단 거리를 구하고 목적지 -> 출발지 최단 거리를 구해야한다.
한 명마다 다익스트라 알고리즘을 2번씩 적용, 즉 총 다익스트라 알고리즘을 2*n만큼 사용한다.
다익스트라 알고리즘은 다음과 같다.
def dijkstra(start, end): #start에서 end로 가는데 걸리는 최소 시간
time = [MAX]*(n+1) #start에서 각 노드까지 가는데 걸리는 최소 시간
time[start] = 0 #시작 노드까지 가는데 걸리는 시간은 0
queue = [] #최소 힙. 튜플의 첫 번째 값은 걸리는 시간, 두 번째 값은 도착 노드
heapq.heappush(queue, (0, start)) #튜플의 첫 번째 값인 걸리는 시간은 start 노드부터 걸리는 시간임
while queue: #큐가 빌 때까지
t, node = heapq.heappop(queue) #가장 적게 걸리는 노드 가져옴. (확정)
if node==end:
return t
if t<=time[node]: #더 적게 걸린다면
for node2, time2 in graph[node]: #node와 연결된 인접 노드들 가져옴
if t+time2<time[node2]: #만약 인접 노드까지의 걸리는 시간이 기존보다 크다면 무시
time[node2]=t+time2 #갱신
heapq.heappush(queue, (t+time2, node2)) #최단 거리를 결정할 후보 노드들을 넣기이전 다익스트라 알고리즘 포스팅을 보면서 이해하면 크게 어렵지 않다.
time = [MAX]*(n+1) #start에서 각 노드까지 가는데 걸리는 최소 시간
time[start] = 0 #시작 노드까지 가는데 걸리는 시간은 0
queue = [] #최소 힙. 튜플의 첫 번째 값은 걸리는 시간, 두 번째 값은 도착 노드
heapq.heappush(queue, (0, start)) #튜플의 첫 번째 값인 걸리는 시간은 start 노드부터 걸리는 시간임
time 배열은 start에서 각 인덱스에 해당하는 노드로 갈 때의 최소 시간이다.
시작 노드에서 시작 노드로 가는 시간은 당연히 0이다.
그리고 최소 힙을 생성하고 (최소 시간, 도착 노드) 순으로 값을 넣는다.
시간을 앞에 넣는 이유는 가장 짧게 걸리는 노드를 꺼내서 해당 노드의 최단 거리를 확정하기 위함이다.
그 다음 반복문을 돌리면 된다.
while queue: #큐가 빌 때까지
t, node = heapq.heappop(queue) #가장 적게 걸리는 노드 가져옴. (확정)
if node==end:
return t
if t<=time[node]: #더 적게 걸린다면
for node2, time2 in graph[node]: #node와 연결된 인접 노드들 가져옴
if t+time2<time[node2]: #만약 인접 노드까지의 걸리는 시간이 기존보다 크다면 무시
time[node2]=t+time2 #갱신
heapq.heappush(queue, (t+time2, node2)) #최단 거리를 결정할 후보 노드들을 넣기우선 가장 처음 최소 힙에서 값을 빼온다면 당연히 시작 노드일 것이다.

A 노드는 시작 노드이기 때문에 최단 거리가 0으로 확정된 상태로 시작한다.
그 다음 node==end 조건문은 우선 생략하고 t<=time[node]부터 설명하겠다.
t는 A의 시간인 0이고 time[A]의 경우 처음에 0으로 세팅을 해두었다. 처음 이 조건문은 조건을 무조건 만족하기 때문에 실행한다.
for node2, time2 in graph[node]: #node와 연결된 인접 노드들 가져옴
if t+time2<time[node2]: #만약 인접 노드까지의 걸리는 시간이 기존보다 크다면 무시
time[node2]=t+time2 #갱신
heapq.heappush(queue, (t+time2, node2)) #최단 거리를 결정할 후보 노드들을 넣기t+time이 time[node2]보다 크다면 무시한다.
그리고 최소 힙에 값을 넣는 것은 최단 거리를 확정할 후보 노드들을 등록하는 것이다.
아래 그림과 같이 후보 노드들을 등록하였다.
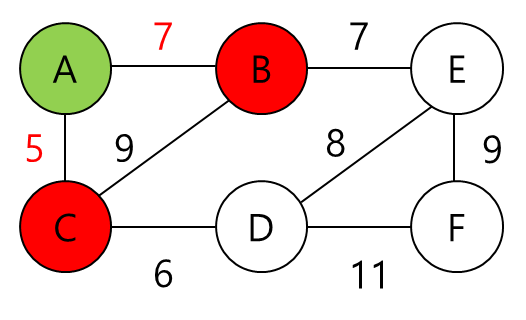
반복문이기 때문에 다시 처음부터 실행한다.
t, node = heapq.heappop(queue) #가장 적게 걸리는 노드 가져옴. (확정)
if node==end:
return t여기서 최소 힙에서 값을 꺼내온다면 후보 노드들 중 가장 거리가 짧은 노드가 나올 것이고 이 노드까지의 최단 거리는 확정된다. (자세한 설명은 위 다익스트라 알고리즘 링크 참고)

이제 node==end 조건문에 대해 설명할 수 있다.
지금까지 A에서 A, C 까지 도달하는 최단 경로는 확정되었다. 더 이상 짧은 거리는 나올 수가 없다.
만약 C가 도착지였다면 node==end 조건문에 걸릴 것이고 이 최단 경로(5)를 반환하면 된다.
다른 모든 노드들을 조사한다고 해서 A-C 최단 경로가 바뀔 일은 없기 때문이다.
우선 설명을 계속하기 위해 이어서 다익스트라 알고리즘을 설명해보겠다.
이제 새롭게 최단 거리가 확정된 노드 C를 기준으로 다시 다음 최단 거리를 확정할 후보 노드들을 등록한다.
if t<=time[node]: #더 적게 걸린다면
for node2, time2 in graph[node]: #node와 연결된 인접 노드들 가져옴
if t+time2<time[node2]: #만약 인접 노드까지의 걸리는 시간이 기존보다 크다면 무시
time[node2]=t+time2 #갱신
heapq.heappush(queue, (t+time2, node2)) #최단 거리를 결정할 후보 노드들을 넣기
거리가 7, 11, 14가 존재한다. 다시 처음으로 돌아가서 최소 힙에서 값을 뺀다면 가장 짧은 거리인 A-B 경로로 B 노드가 확정될 것이다.
만약 B가 목적지였다면 해당 거리를 바로 반환한다.
t, node = heapq.heappop(queue) #가장 적게 걸리는 노드 가져옴. (확정)
if node==end:
return t
참고로 현재 A-B 최단 경로가 확정되었다. 그런데 아직도 후보에는 A-C-B로 가는 경로가 등록되어있다.
당연하게도 이 A-C-B 경로가 최단 경로가 될 일은 없기 때문에 필요가 없다.
언젠가 이 경로가 최소 힙에서 나오게 될텐데 아래 조건문에서 어차피 걸러지기 때문에 신경쓰지 않는다.
time[B]는 이미 최단 경로가 확정되었기 때문이다.
if t<=time[node]: #더 적게 걸린다면
이제 새롭게 최단 거리가 확정된 노드 B를 기준으로 다시 다음 최단 거리를 확정할 후보 노드들을 등록한다.
if t<=time[node]: #더 적게 걸린다면
for node2, time2 in graph[node]: #node와 연결된 인접 노드들 가져옴
if t+time2<time[node2]: #만약 인접 노드까지의 걸리는 시간이 기존보다 크다면 무시
time[node2]=t+time2 #갱신
heapq.heappush(queue, (t+time2, node2)) #최단 거리를 결정할 후보 노드들을 넣기
이 과정을 계속 반복하면 된다.
이 과정을 한 사람당 두 번씩 반복해서 가장 오래 걸리는 시간을 찾아내면 된다.
result = 0
for i in range(1, n + 1):
res = dijkstra(i, x)
result = max(result, dijkstra(i, x)+dijkstra(x, i))
print(result)<최종 코드>
import sys
import heapq
input=sys.stdin.readline
MAX=1e9
n, m, x = map(int, input().split())
graph=[[] for _ in range(n+1)] #그래프
for _ in range(m): #거리 넣기
a, b, t = map(int, input().split())
graph[a].append((b, t)) #a에서 b로 가는데 t시간이 걸림
def dijkstra(start, end): #start에서 end로 가는데 걸리는 최소 시간
time = [MAX]*(n+1) #start에서 각 노드까지 가는데 걸리는 최소 시간
time[start] = 0 #시작 노드까지 가는데 걸리는 시간은 0
queue = [] #최소 힙. 튜플의 첫 번째 값은 걸리는 시간, 두 번째 값은 도착 노드
heapq.heappush(queue, (0, start)) #튜플의 첫 번째 값인 걸리는 시간은 start 노드부터 걸리는 시간임
while queue: #큐가 빌 때까지
t, node = heapq.heappop(queue) #가장 적게 걸리는 노드 가져옴. (확정)
if node==end:
return t
if t<=time[node]: #더 적게 걸린다면
for node2, time2 in graph[node]: #node와 연결된 인접 노드들 가져옴
if t+time2<time[node2]: #만약 인접 노드까지의 걸리는 시간이 기존보다 크다면 무시
time[node2]=t+time2 #갱신
heapq.heappush(queue, (t+time2, node2)) #최단 거리를 결정할 후보 노드들을 넣기
result = 0
for i in range(1, n + 1):
res = dijkstra(i, x)
result = max(result, dijkstra(i, x)+dijkstra(x, i))
print(result)