백준 1080번과 2138번 모두 그리디 알고리즘으로 풀이가 비슷해서 같이 가져와보았다.
그리디 알고리즘은 욕심쟁이 알고리즘이라고도 하는데 현재 최선의 선택을 하는 것이다.
미래를 생각하지 않고 현재 선택할 수 있는 경우의 수 중 최선의 선택을 하는 것인데 반드시 최적의 해를 구할 것이라는 보장이 없다.
최적의 해를 구하지 못하더라도 근사값은 구할 수 있기 때문에 유용한 알고리즘이다.
그리디 알고리즘을 사용했을 때 최적의 해를 보장할 수 있으려면 다음과 같은 조건이 필요하다.
탐욕 알고리즘이 잘 작동하기 위한 조건은
탐욕스런 선택 조건(greedy choice property)과 최적 부분 구조 조건(optimal substructure)이다.
탐욕스런 선택 조건은 앞의 선택이 이후의 선택에 영향을 주지 않는다는 것이며,
최적 부분 구조 조건은 문제에 대한 최적해가 부분문제에 대해서도 역시 최적해라는 것이다.
<1080 행렬>
https://www.acmicpc.net/problem/1080
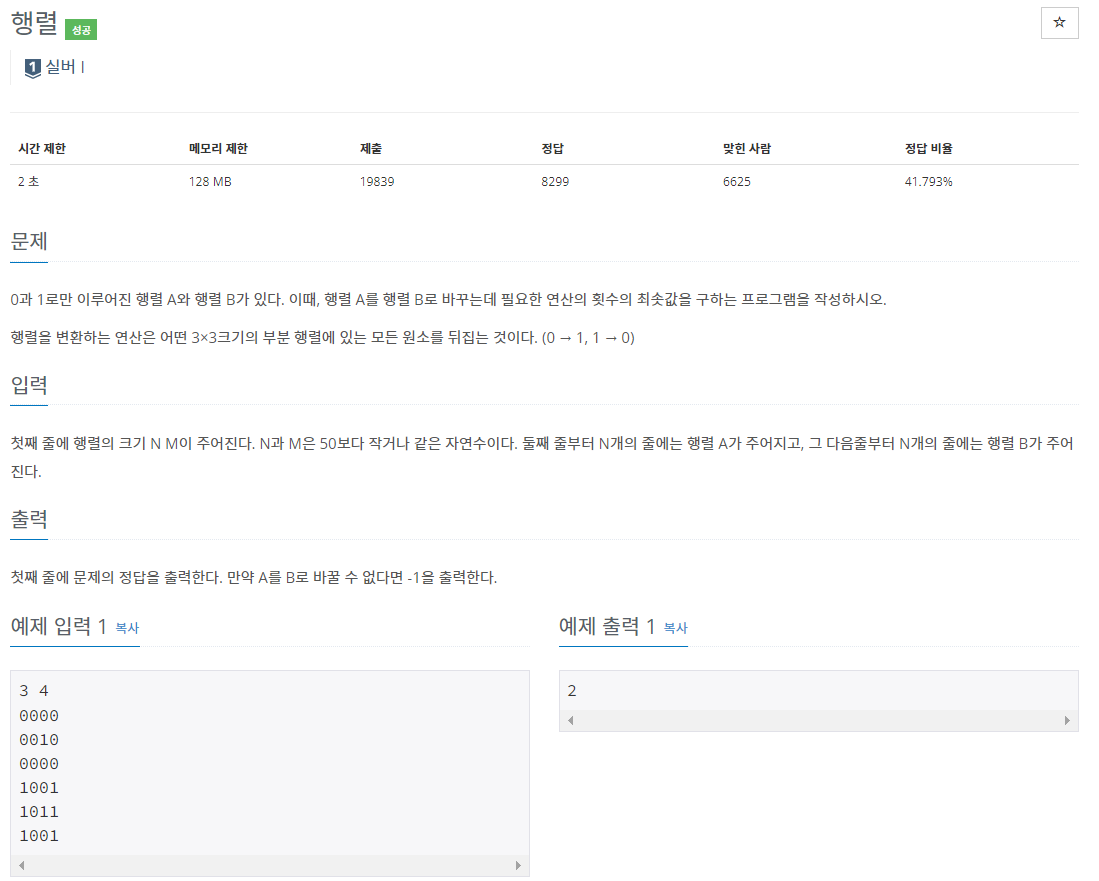
1080번: 행렬
첫째 줄에 행렬의 크기 N M이 주어진다. N과 M은 50보다 작거나 같은 자연수이다. 둘째 줄부터 N개의 줄에는 행렬 A가 주어지고, 그 다음줄부터 N개의 줄에는 행렬 B가 주어진다.
www.acmicpc.net
모든 행렬의 요소들을 순회하면서 그리디 알고리즘을 적용한다.
matrix[a][b]의 값을 확인해보고 바꿔야한다면 (a, b)가 3x3 정사각형의 좌측 상단의 점이라고 가정하고 행렬을 변형하는 것이다.
이를 위해서 나는 새로운 행렬을 만들었다. 값이 1이라면 변경되어야 하고 0이라면 변경되면 안된다.
matrix=[[0]*m for _ in range(n)]
for i in range(n):
for j in range(m):
if matrix_a[i][j]!=matrix_b[i][j]:
matrix[i][j]=1그런데 변형할 3x3 행렬 안에 변경되면 안되는 0이라는 값이 있다면 이는 1로 변경될 것이다.
그래도 상관이 없는게 어차피 순회를 하다보면 언젠가 이 변경된 값에 도달하게 될테고 그 때의 값이 0이냐 1이냐에 따라 변형 여부를 선택하면 된다.
다음 그림과 같은 과정들을 반복한다.

<최종 코드>
import sys
input=sys.stdin.readline
n, m = map(int, input().split())
matrix_a = [list(input().rstrip()) for _ in range(n)]
matrix_b = [list(input().rstrip()) for _ in range(n)]
#A의 각 요소들이 바뀌어야하는 횟수. 정확히는 짝수번이냐 홀수번이냐. 1번이면 홀수, 0번이면 짝수
matrix=[[0]*m for _ in range(n)]
for i in range(n):
for j in range(m):
if matrix_a[i][j]!=matrix_b[i][j]:
matrix[i][j]=1
cnt=0 # 변형 횟수
for i in range(n-2):
for j in range(m-2):
if matrix[i][j]==1:
cnt+=1
for a in range(i,i+3):
for b in range(j, j+3):
matrix[a][b] = 0 if matrix[a][b]==1 else 1
for i in range(n):
for j in range(m):
if matrix[i][j]==1:
print(-1)
exit()
print(cnt)
<2138 전구와 스위치>
https://www.acmicpc.net/problem/2138
2138번: 전구와 스위치
N개의 스위치와 N개의 전구가 있다. 각각의 전구는 켜져 있는 상태와 꺼져 있는 상태 중 하나의 상태를 가진다. i(1 < i < N)번 스위치를 누르면 i-1, i, i+1의 세 개의 전구의 상태가 바뀐다. 즉, 꺼져
www.acmicpc.net

이 문제는 n번 스위치를 누르면 n-1, n, n+1번 전구와 영향을 받는 문제이다.
행렬 문제와 동일한 풀이를 사용하면 문제가 발생한다.
i번째 스위치를 누르지 않기로 결정했는데 i+1번째 스위치를 누르게 되어 i번째 스위치를 다시 눌러야 할 수도 있기 때문이다.
그래서 문제의 변형이 필요하다. n-1, n, n+1번 전구가 영향을 받도록 하는게 아니라 n, n+1, n+2 전구가 영향을 받도록 변형하는 것이다.
그런데 이렇게 변형하면 가장 첫 번째 스위치에서 예외가 발생한다.
첫 번째 스위치는 0번 전구와 1번 전구에 영향을 주기 때문에 첫 번째 스위치를 누르는 경우와 누르지 않는 경우 두 가지를 고려해서 문제를 풀어야 한다.
이는 단순하게 배열의 첫 부분에 0과 1을 각각 추가하는 방식으로 해결할 수 있다.
<최종 코드>
import sys
input=sys.stdin.readline
n=int(input())
bulb=list(input().rstrip())
switch=list(input().rstrip())
#전구의 상태를 홀수번 바꿔야하면 1 짝수번 바꿔야하면 0
arr=[
1 if bulb[i]!=switch[i] else 0
for i in range(n)
]
#n-1, n, n+1 문제를 n, n+1, n+2로 변형한다.
#그래서 맨 앞에 0을 넣은 것 한 번, 1을 넣은 것 한 번 총 두 번을 실시한다.
arr_temp=[0]+arr
cnt_1=0 #변형 횟수
possible_1=True # 가능 여부
for i in range(n-1):
if arr_temp[i]==1:
cnt_1+=1
for j in range(i, i+3):
arr_temp[j]=0 if arr_temp[j]==1 else 1
if arr_temp[n-1]!=arr_temp[n]: #불가능한 상황
possible_1=False
elif arr_temp[n-1]==1 and arr_temp[n]==1: #둘 다 1이면 한 번 더 바꿔야하곡 둘 다 0이면 끝
cnt_1+=1
arr_temp=[1]+arr
cnt_2=0 #변형 횟수
possible_2=True # 가능 여부
for i in range(n-1):
if arr_temp[i]==1:
cnt_2+=1
for j in range(i, i+3):
arr_temp[j]=0 if arr_temp[j]==1 else 1
if arr_temp[n-1]!=arr_temp[n]: #불가능한 상황
possible_2=False
elif arr_temp[n-1]==1 and arr_temp[n]==1: #둘 다 1이면 한 번 더 바꿔야하곡 둘 다 0이면 끝
cnt_2+=1
if possible_1 and possible_2: #둘 다 가능하다면 작은 값
print(min(cnt_1, cnt_2))
elif possible_1: #1번만 가능하다면
print(cnt_1)
elif possible_2: #2번만 가능하다면
print(cnt_2)
else: #둘 다 안된다면
print(-1)'백준 알고리즘' 카테고리의 다른 글
| [CodeTree] 우리는 하나 (0) | 2024.08.17 |
|---|---|
| [백준 16500][파이썬] 문자열 판별 (dfs) (0) | 2023.07.06 |
| [백준 10473][파이썬] 인간 대포 (우선순위 큐를 사용하지 않는 다익스트라) (0) | 2023.06.29 |
| [백준 11657][파이썬] 타임 머신 (벨만 포드) (0) | 2023.06.13 |
| [백준 4485][파이썬] 녹색 옷 입은 애가 젤다지? (다익스트라) (0) | 2023.06.09 |