2023. 10. 16. 12:00ㆍ공부/보안
암호의 기본 연산은 문자를 다른 문자로 바꾸는 "치환"과 문자의 순서를 재배치하는 "전치" 방식이다.
이번 시간에는 치환 방식을 사용하는 고전 암호 기법에 대해서 알아보려고 한다.
Caesar 암호
Caesar 암호는 치환 방식의 대표적인 암호 방식이다.
모든 알파벳들을 자신보다 문자 뒤에 있는 문자로 치환하는 방식이다.
| 평문 | a | b | c | d | e |
| 암호문 | d | e | f | g | h |
a에서 z까지 0부터 차례대로 숫자를 매칭했다고 하자.
매칭한 숫자를 바탕으로 암호화 알고리즘과 복호화 알고리즘을 다음과 같이 표현할 수 있다.
C = E(k, p) = (p + k) mod 26 (암호화 알고리즘)
D = E(k, C) = (C - k) mod 26 (복호화 알고리즘)
k는 키 값을 의미하는데 caesar에서는 3을 키 값으로 정한 것이다.
그런데 이 caesar 방식은 가능한 키의 종류가 26가지밖에 되지 않기 때문에 모든 키를 대입하는 전사적 키 해독 기법에 취약하다.
전사적 키 해독 기법의 위험에 벗어나기 위해서는 키 공간의 크기가 커야 한다.
단일 문자 치환 암호 기법
단일 문자 치환 암호 기법은 문자를 임의의 문자로 치환하는 방식이다.
다음은 단일 문자 치환 암호 기법 키의 예시이다.
| 평문 | a | b | c | d | ... |
| 암호문 | d | e | a | z | ... |
자신의 임의대로 치환할 수 있기 때문에 키 공간의 크기는 26! 이다.
caesar 방식에 비해서 키 공간의 크기가 크기 때문에 전사적 키 해독의 위험에서 벗어날 수 있다.
그러나 언어의 규칙성을 이용한 공격에 취약하다.
다음은 영문자의 상대 등장 빈도이다.

e와 t가 가장 많이 나오는 것을 확인할 수 있다.
이러한 언어의 규칙성을 이용해서 암호문의 모든 알파벳 등장 횟수를 계산해서 위 표에 대입하는 공격을 사용할 수 있다.
play fair
지금까지는 단일 문자를 암호화하는 방식에 대해서 알아보았다.
play fair 암호는 다중 문자를 암호화하는 방식이다.
키워드가 monarchy라고 하자.
5x5 크기의 행렬을 만들어서 키워드 순서대로 넣는다. (만약 중복된 문자가 있다면 키워드에 중복된 문자가 없도록 제거한다.)
| m | o | n | a | r |
| c | h | y | ||
그리고 남은 알파벳의 순서대로 나머지를 채워넣는다. ( i와 j는 같은 문자로 취급한다.)
| m | o | n | a | r |
| c | h | y | b | d |
| e | f | g | i/j | k |
| l | p | q | s | t |
| u | v | w | x | z |
이렇게 테이블을 만들었다면 다음과 같은 암호화 방식을 적용한다.
평문은 balloon이라고 하자.
1. 두 문자씩 나눈다.
ba / ll / oo / n
2. 중복된 값에 x를 넣는다.
ba / lx / ox / n
3. 만약 마지막으로 나눈 문자가 2개가 아니라면 x를 추가한다.
ba / lx / ox / nx
이렇게 평문을 전처리하고 테이블을 보고 암호화를 진행해보자.
평문 : ba
| m | o | n | a | r |
| c | h | y | b | d |
| e | f | g | i/j | k |
| l | p | q | s | t |
| u | v | w | x | z |
이렇게 두 문자가 같은 열에 있다면 한 칸씩 내린다. (
| m | o | n | a | r |
| c | h | y | b | d |
| e | f | g | i/j | k |
| l | p | q | s | t |
| u | v | w | x | z |
ba(평문) => ib(암호문)
만약 x와 같이 마지막을 한 칸 내리려고 한다면 처음으로 돌아간다.
다음 lx를 암호화 해보자.
평문 : lx
| m | o | n | a | r |
| c | h | y | b | d |
| e | f | g | i/j | k |
| l | p | q | s | t |
| u | v | w | x | z |
두 문자가 같은 열, 같은 행에 있지 않으면 짝을 찾아서 암호화한다.
| m | o | n | a | r |
| c | h | y | b | d |
| e | f | g | i/j | k |
| l | p | q | s | t |
| u | v | w | x | z |
lx(평문) => us(암호문)
balloon에는 존재하지 않지만 같은 행에 있는 경우도 암호화 해보자.
예를 들어 ch를 암호화 해보자.
| m | o | n | a | r |
| c | h | y | b | d |
| e | f | g | i/j | k |
| l | p | q | s | t |
| u | v | w | x | z |
이렇게 같은 행에 있을 때는 오른쪽으로 이동한다.
| m | o | n | a | r |
| c | h | y | b | d |
| e | f | g | i/j | k |
| l | p | q | s | t |
| u | v | w | x | z |
d와 같이 마지막에 있는 문자를 오른쪽으로 옮길 때는 처음으로 돌아간다.
이러한 play fair의 키 공간의 크기는 26 x 26 = 676이다.
hill 암호
hill 암호는 행렬 연산을 통해 암호화를 진행한다.
모든 알파벳을 숫자에 매치한다.
간단하게 a부터 z까지 차례대로 0부터 25까지 매치해보자.
pay는 [15, 0, 24] 로 나타낼 수 있다.
그리고 키를 다음과 같이 행렬로 나타내보자.
| 17 | 17 | 5 |
| 21 | 18 | 21 |
| 2 | 2 | 19 |
평문 행렬을 P라고 하고 키 행렬을 K라고 한다면 암호문 행렬 C는 C = PK mod 26으로 표현할 수 있다.
행렬 연산을 해보면
C = [ (15*17 + 0*21 + 24*2) mod 26, (15*17 + 0*18, 24*2) mod 26, (24*5 + 0*21 + 24*19) mod 26 ]
= [ 17, 17, 11 ]
이제 다시 숫자를 알파벳으로 바꾸면 rrl이 된다.
복호화를 위한 식은 다음과 같다.
P = CK^(-1) mod 26
vigenere
기존 단일 문자 암호 방식은 언어의 특성을 이용한 공격에 취약하다.
그런데 위에서 배웠던 play fair와 같은 다중 문자 방식은 이러한 위험에서 조금 벗어날 수 있다.
vigenere 방식도 play fair와 같은 다중 문자 방식이다.
vigenere 방식의 키, 암호화, 복호화 알고리즘을 살펴보자.
K = K(1) K(2) K(3) K(4) ... K(m-1)
C(i) = ( P(i) + K(i mode m) ) mod 26
P(i) = ( C(i) - K(i mode m) ) mod 26
우선 키워드를 HELLO라고 해보자.
그리고 암호화할 평문을 PLAINTEXT라고 해보자.
키워드를 이어붙여서 평문의 길이만큼 만들어보자.
| 평문 | P | L | A | I | N | T | E | X | T |
| 키 | H | E | L | L | O | H | E | L | L |
이를 바탕으로 암호화를 진행하면 된다.
위와 같이 보면 어렵지만 vigenere 암호 방식은 vigenere square를 작성하면 쉽게 확인할 수 있다.
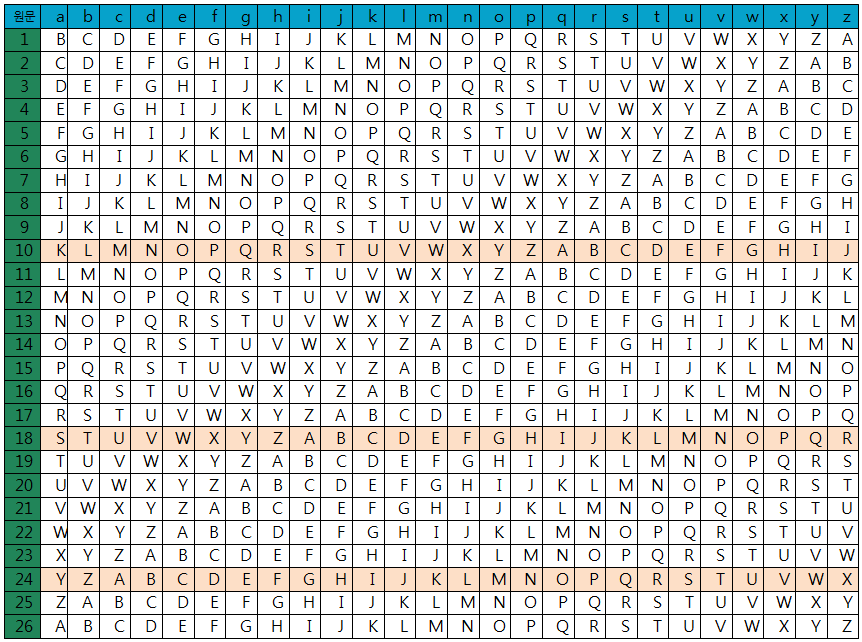
첫 번째 문자를 암호화해보면 평문이 P, 키가 H에 해당하는 값은 W이다.
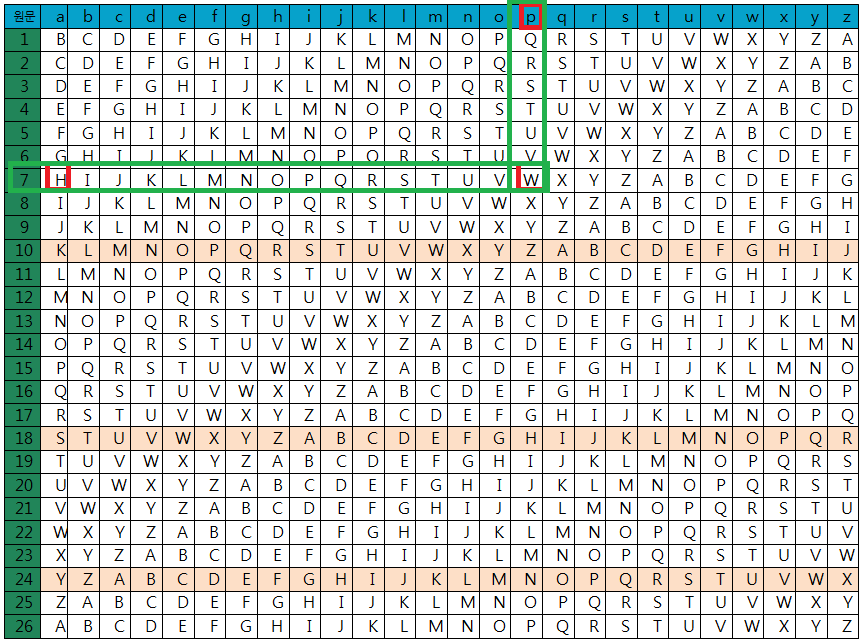
즉 P를 W로 바꾸면 된다.
이 과정을 반복한다.
vernam
vernam 암호화 방식은 알파벳을 그대로 사용하는 것이 아니라 2진수로 바꿔서 사용한다.
그리고 알파벳은 2진수로 만들어서 xor 연산을 진행한다.
Ci = Pi xor Ki
Pi = Ci xor Ki
one time pad
one time pad 암호화 방식은 vigenere와 다르게 키워드를 반복해서 키를 만들지 않고 평문의 길이만큼 긴 키를 사용한다.
one time pad 암호화 방식은 통계적인 공격에서 벗어날 수 있다.
그런데 큰 용량의 random한 key를 사용하기가 어렵고 키 분배와 보호가 어렵다.
'공부 > 보안' 카테고리의 다른 글
| [보안] SSL/TLS 인증서 발급 과정 및 인증 절차 (0) | 2023.10.30 |
|---|---|
| [보안] 대칭키, 비대칭키(공개키), 혼합 (0) | 2023.10.28 |
| [정보 보안] 블록 암호와 DES (feistel) (1) | 2023.10.19 |
| [정보 보안] 고전 암호 기법 (전치) (1) | 2023.10.17 |