https://www.acmicpc.net/problem/1520

풀이
굉장히 어려웠던 문제입니다.
DFS와 메모이제이션 기법을 적절히 사용해야 하는 문제였습니다.
풀이를 생각하지 못 하고 검색을 통해 해결했습니다.
첫 번째는 완전 탐색을 떠올렸습니다.
DFS와 백트래킹 기법을 사용해서 완전 탐색을 하면 갈 수 있는 길의 개수를 구할 수 있습니다.
하지만 N과 M의 최대 크기는 500이었고 최대 칸의 개수는 250,000이었기 때문에 시간 초과가 발생합니다.
두 번째는 DP를 떠올렸습니다.
dp[x][y]를 "좌표 (x, y)까지 도착할 수 있는 경우의 수"라고 정의하면 문제를 해결할 수 있을 것 같았습니다.
그래서 (0, 0)부터 (n-1, m-1)까지 dp 값을 구하면 해결할 수 있을 것 같았는데 문제는 갈 수 있는 방향이 고정되어 있지 않다는 점이었습니다.
이 방법은 갈 수 있는 방향이 오른쪽 혹은 아래로 고정되어 있었다면 적용할 수 있지만 4방향 모두 탐색할 수 있기 때문에 dp를 적용할 수 없었습니다.
이 문제는 제가 떠올린 첫 번째와 두 번째 방법을 적절히 조합하면 풀 수 있습니다.
바로 DFS + 백트래킹을 사용하되 이미 방문했고 경로가 확정난 칸은 다시 방문하지 않는 것입니다.
여기서 방문했다는 뜻은 DFS + 백트래킹 기법으로 이미 방문 한 곳을 의미하고 경로가 확정났다는 뜻은 해당 칸에서 도착 지점까지 갈 수 있다는 것을 의미합니다.
아래 그림을 보면 좌측 하단은 방문했지만 해당 칸으로부터 도착 지점까지 갈 수 없는 칸을 의미하고 이는 방문했고 경로 확정이 나지 않은 칸입니다.
방문했고 경로 확정이 나지 않은 칸은 해당 칸으로부터 도착 지점까지 갈 수 없는 칸을 의미하기도 하지만 갔다가 아직 돌아오지 않은 칸을 의미하기도 합니다.
두 경우 모두 다시 방문할 필요가 없다는 것은 동일합니다.
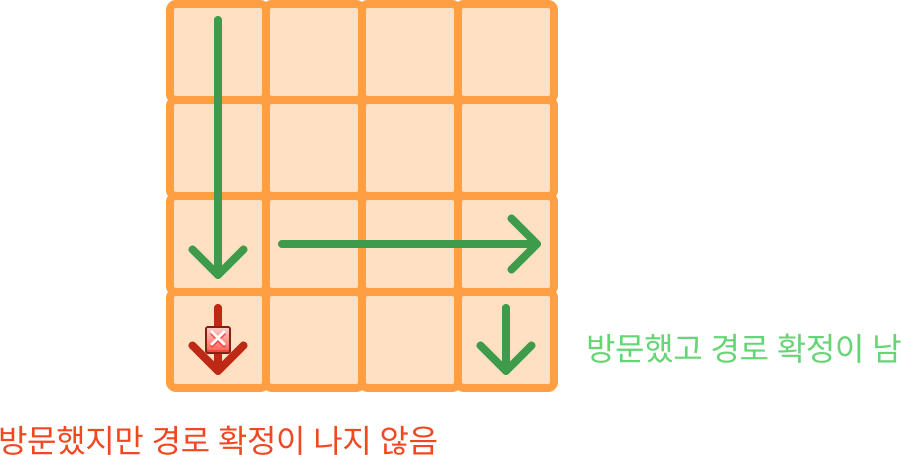
그런데 초록색 화살표가 방문한 칸들은 해당 칸으로부터 도착 지점까지 갈 수 있는 칸을 의미하고 이는 방문했고 경로 확정이 난 칸입니다.
일반적인 DFS + 백트래킹 기법에서는 칸을 방문한 뒤 다시 돌아올 때 방문 여부를 false로 바꾸어서 다른 경로에서 해당 칸에 방문할 수 있도록 구현합니다.
하지만 이 문제에서는 방문 여부를 false로 바꿀 필요가 없습니다.
칸을 방문했는데 이미 방문한 칸이면서 경로가 확정이 났다면 무조건 도착 지점까지 갈 수 있다는 것을 의미합니다.
문제가 원하는 답은 도착 가능한 경로의 개수이기 때문에 각 칸마다 도착 가능한 경로의 개수를 구해야 합니다.
코드
import java.io.IOException;
import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.util.Stack;
import java.util.StringTokenizer;
public class Main{
// 동서남북
public static int[] dx = {0, 0, 1, -1};
public static int[] dy = {1, -1, 0, 0};
public static int[][] map;
public static int[][] arr;
public static boolean[][] visited;
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken());
int m = Integer.parseInt(st.nextToken());
map = new int[n][m];
arr = new int[n][m];
visited = new boolean[n][m];
for (int i=0; i<n; i++){
st = new StringTokenizer(br.readLine());
for (int j=0; j<m; j++){
map[i][j] = Integer.parseInt(st.nextToken());
}
}
arr[n-1][m-1] = 1;
visited[n-1][m-1] = true;
bw.write(String.valueOf(getTotalWayCount(0, 0)));
bw.close();
}
public static int getTotalWayCount(int x, int y){
if (x == map.length-1 && y == map[0].length-1){
visited[x][y] = true;
return arr[x][y];
}
// 4방향 탐색
for (int i=0; i<4; i++){
int nx = x+dx[i];
int ny = y+dy[i];
// 범위 넘어가면 스킵
if (nx<0 || nx>=map.length || ny <0 || ny>=map[0].length){
continue;
}
// 갈 수 없는 곳이면 스킵
if (map[nx][ny] >= map[x][y]){
continue;
}
// 방문을 했지만 아직 경로가 확정나지 않은 경우 스킵
if (visited[nx][ny] && arr[nx][ny] == 0){
continue;
}
// 방문을 했고 이미 경로가 확정난 경우
if (visited[nx][ny] && arr[nx][ny] > 0){
// 다시 방문할 필요가 없다.
arr[x][y]+=arr[nx][ny];
continue;
}
// 방문을 했고 경로가 아직 확정 안 났다면 방문
visited[nx][ny] = true;
arr[nx][ny] = getTotalWayCount(nx, ny);
arr[x][y] += arr[nx][ny];
}
return arr[x][y];
}
}
'백준 알고리즘 > dp' 카테고리의 다른 글
| [백준 20667][java] 크롬 (0) | 2025.03.03 |
|---|---|
| [백준 15486][JAVA] 퇴사 2 (1) | 2025.02.15 |
| [백준 9251][파이썬] LCS (최장 공통 부분 수열) (0) | 2023.03.18 |
| [백준 11066][파이썬] 파일 합치기 (dp 알고리즘) (0) | 2023.03.15 |
| [백준 2839][파이썬] 설탕 배달 (0) | 2023.01.23 |