문자열 알고리즘이란 어떤 문자열에서 원하는 패턴을 찾는 알고리즘이다.
문자열의 부분 문자열과 패턴을 비교하면서 패턴의 존재 여부를 알 수 있다.
예를 들어서 "banana"에서 "ana"라는 패턴을 찾고자한다면 "banana", "banana"
이렇게 총 두 개가 존재함을 알 수 있다.
그러나 모든 부분 문자열과 패턴을 비교한다면 엄청난 시간이 걸릴 것이다.
그래서 KMP 알고리즘을 사용하면 패턴 비교시간을 줄일 수 있다.
KMP 알고리즘의 필요성
굉장히 긴 문자열이 존재하고 이 문자열에서 "abcac"라는 문자열을 찾고 싶다고하자.

패턴을 찾는 와중에 위와 같은 상황이 발생했다고 하자. abca까지는 맞았으나 그 다음 문자열에서 찾고있는 패턴이 아님을 알아냈다.

그럴 경우 패턴을 한 칸 옆으로 옮겨서 다시 패턴 일치 여부를 확인할 것이다.
그런데 이렇게 한 칸씩 옮기게되면 문자열과 패턴의 길이가 길어질수록 많은 시간이 걸릴 것이다.
그래서 옮길 수 있는 만큼 최대한 많이 옮기는 것이 효율적인 방법이다.
위의 상황의 경우 한 칸만 옮기는 것이 아니라 아래처럼 3칸을 옮길 수 있다.

문자열과 패턴의 매칭이 실패했을 때 매칭을 성공했던 부분을 다시 재활용하는 것이 KMP 알고리즘이다.
용어
KMP 알고리즘을 공부하기에 앞서 용어부터 정의해야 한다.
접두사 : 문자열의 첫 부분부터 시작하는 부분 문자열
예를 들어 "abcab"라는 패턴의 접두사는 "abcab", "abcab", "abcab", "abcab", "abcab" 에서 빨간색인 부분이다.
접미사 : 문자열의 마지막 부분으로 끝나는 부분 문자열
"abcab"라는 패턴의 접미사는 "abcab", "abcab", "abcab", "abcab", "abcab" 에서 빨간색인 부분이다.
실패 함수 : 어떠한 문자열에서 접두사와 접미사가 같은 부분 문자열 중에서 길이가 가장 긴 것
예를 들어서 "abcdabc"에서 실패 함수는 3이다.

f(x)를 패턴에서 첫 번째부터 x번째까지의 부분 문자열의 실패 함수라고 정의한다.
"abcdabc"라는 패턴에서 f(2)가 의미하는 바는 "ab"라는 문자열에서 접두사와 접미사가 같은 부분 문자열 중에서 길이가 가장 긴 것이다. 0이 될 것이다.
그렇다면 f(6)이 의미하는 바는 "abcdab"라는 문자열에서 접두사와 접미사가 같은 부분 문자열 중에서 길이가 가장 긴 것이다. 2가 될 것이다.
그렇다면 f(7)이 의미하는 바는 "abcdabc"라는 문자열에서 접두사와 접미사가 같은 부분 문자열 중에서 길이가 가장 긴 것이다. 3이 될 것이다.
실패 함수를 바탕으로 매칭에 실패했을 때 최대 옮길 수 있는 횟수를 알 수 있다.
패턴의 n번째 문자에서 매칭을 실패했다. 그렇다면 우리는 옮길 수 있는 최대 횟수를 n-f(n)이라고 정의할 수 있다.
이제 아래와 같은 상황이 발생했다 해보자,

7번째 문자에서 매칭을 실패했으므로 7-f(7) = 4 즉 4번 옮길 수 있다.
아래 상황과 같은 예시를 하나 더 들어보자.

이번엔 6번째 문자에서 실패를 했으므로 6-f(6)= 4 즉 4번 옮길 수 있다.
이렇듯 길이가 n인 패턴이 존재한다고 하면 이 패턴의 각각의 요소에 대한 모든 실패 함수를 구해야한다.
즉 f(1)부터 f(n)까지 구해야한다.
이렇게 한 번 실패 함수들을 구하고 나면 문자열 매칭에 실패할 때마다 더 많이 옮겨서 비교할 수 있다.
실패 함수 구하기
실패 함수도 무작정 구해서는 안된다. 자칫하다간 실패 함수를 구하는 과정에서 엄청난 시간을 소비할 수 있기 때문이다.
길이가 n인 문자열에서 총 n개의 실패 함수를 구해야한다. 실패 함수 구하는 과정도 이전에 구했던 실패 함수를 이용하면 시간을 단축할 수 있다.
"abcdabc" 패턴의 실패 함수를 f(1)부터 f(6)까지 구한 상황이고 f(7)을 구해야하는 상황을 가정해보자.

f(6)까지 구한 상황이고 f(6)의 값은 2이다.
이 의미는 1번째 2번째 문자열이 5번째 6번째 문자열과 같다는 뜻이다.
이제 f(7)을 구해야하는데 이는 ( f(6)+1 )번째 문자와 7번째 문자를 비교하면 된다.
3번째 문자와 7번째 문자를 비교하면 같으므로 f(7)의 값은 2+1=3이 된다.
f(n)을 구하기 위해서 ( f(n-1)+1 )번째 문자와 n번째 문자를 비교하는 것이다.
같을 경우 f(n) = f(n-1) + 1이 된다.
같지 않다면 (f( f( n-1 ) ) +1)번째 문자와 n번째 문자를 비교한다.
비교한 결과가 같다면 f(n) = f( f( n-1 ) ) +1이 된다.
만약 끝까지 같지 않다면 첫 번째와 비교하게 될 것이고 첫 번째와 같다면 f(n)=1 아니면 f(n)=0이다.
"aabaaa"의 실패 함수를 구하는 과정은 다음과 같다.
먼저 f(1)은 무조건 0이다.
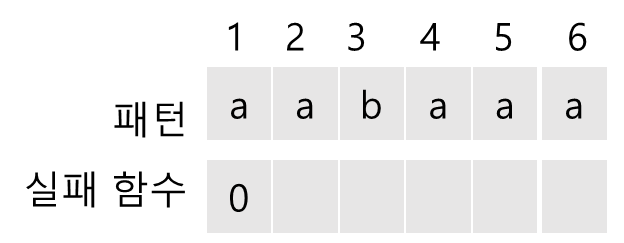
f(2)를 구하기 위해서 ( f(1)+1=1 )번째와 2번째 문자를 비교한다. 같으므로 f(2)=f(1)+1=1이다.

f(3)을 구하기 위해서 ( f(2)+1=2 )번째와 3번째 문자를 비교한다. 다르므로 ( f( f(2) ) + 1 = 1)번째 문자와 3번째 문자를 비교한다.
첫 번째 문자와 비교했을 땐 같으면 1 아니면 0이다. 같지 않으므로 f(3) = 0이다.
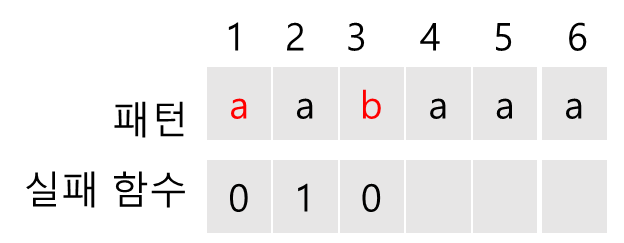
f(4)를 구하기 위해서 ( f(3)+1=1 )번째와 4번째 문자를 비교한다. 같으므로 f(4) = f(3)+1 = 1이다.
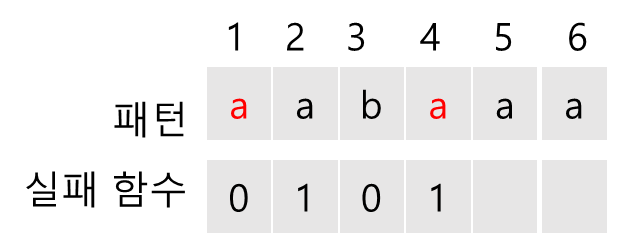
f(5)를 구하기 위해서 ( f(4)+1=2 )번째와 5번째 문자를 비교한다. 같으므로 f(5) = f(4)+1 = 2이다.
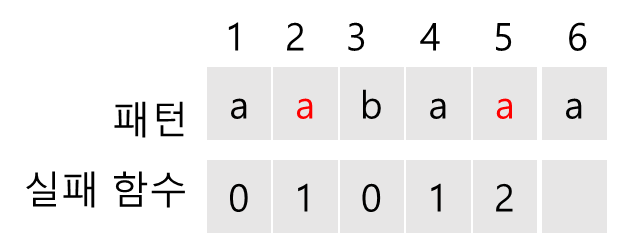
f(6)을 구하기 위해서 ( f(5)+1=3 )번째와 6번째 문자를 비교한다. 다르므로 ( f( f(5) ) + 1 = 2)번째 문자와 6번째 문자를 비교한다.

같으므로 f(6) = f (f(5)) + 1 = 2가 된다.

이렇게 KMP 알고리즘과 실패 함수를 구하는 방법을 알아보았다.
'공부 > Algorithm' 카테고리의 다른 글
| [Algorithm] RMQ (Range Minimum Query) (0) | 2023.04.19 |
|---|---|
| [Algorithm] 다익스트라 (Dijkstra algorithm), 벨만 포드(Bellman ford algorithm) (0) | 2022.12.19 |
| [Algorithm] 프림 알고리즘(Prim algorithm)과 크루스칼 알고리즘 (Kruskal algorithm) (0) | 2022.12.17 |
| [Algorithm] 점화식 점근적 접근 방식(반복 대치, 추정 후 증명) (0) | 2022.12.05 |
| [Algorithm] 없는 숫자 찾기 (0) | 2022.12.04 |