https://www.acmicpc.net/problem/25682
25682번: 체스판 다시 칠하기 2
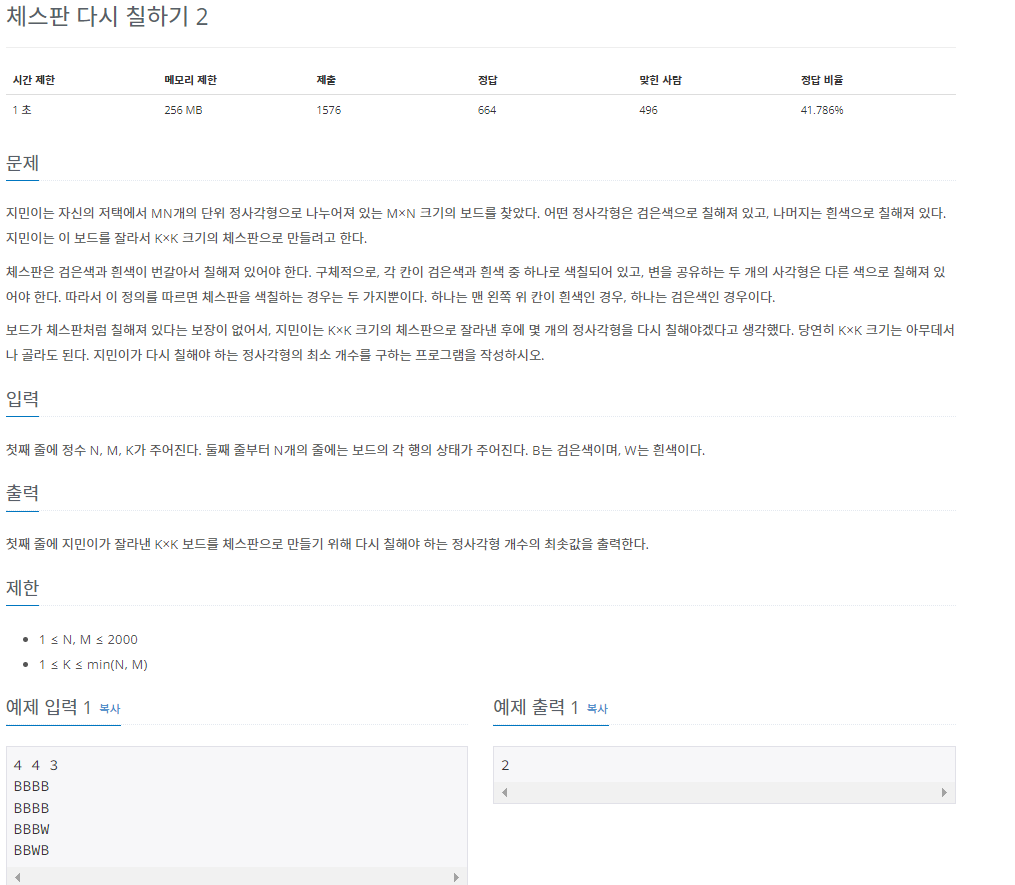
첫째 줄에 정수 N, M, K가 주어진다. 둘째 줄부터 N개의 줄에는 보드의 각 행의 상태가 주어진다. B는 검은색이며, W는 흰색이다.
www.acmicpc.net
백준 1018번 문제와 유사한 문제이다.
https://growth-coder.tistory.com/87
이 문제는 입력 값의 범위가 크지 않았기 때문에 그냥 올바른 체스판 하나를 만들고 하나하나 비교해가면서 바꿔야하는 칸의 개수를 구했다.
그러나 이 문제는 값의 범위도 크고 주어진 체스판을 잘라서 바꿔야하는 칸의 개수를 구해야하기 때문에 위와 동일한 방식으로 풀면 너무 오랜 시간이 걸린다.
이 문제는 누적 합 알고리즘을 사용해서 시간을 단축할 수 있다.
핵심 알고리즘
5x5 체스판 하나가 주어진 상황을 생각해보자.
그리고 s[ i ] [ j ]를 왼쪽 모서리 끝부터 i행 j열 까지 자른 체스판이 올바른 체스판이 되기 위해 바꿔야하는 칸의 최소 개수라고하자.
그러면 s[3][4]는 아래 체스판의 노란색 부분에 해당하는 체스판이 올바른 체스판이 되기 위해 바꿔야하는 칸의 최소 개수가 될 것이다.

그리고 s[4][5]를 구하려 한다면 s[3][4]의 값과 빨간 부분과 파란 부분에 해당하는 값을 더해야 할 것이다.

나는 빨간색 행을 row_sum이라고 하고 빨간색 열을 col_sum이라고 하여 값을 계속 누적하여 구했다.
모든 좌표에 대해서 값을 구했다면 ( 1, 1 )에서 ( 4, 4 )에 해당하는 만큼 잘라서 해당 체스판이 올바른 체스판이 되려면 바꿔야하는 칸의 개수는 s[4][4] - s[1][4] - s[4][1] + s[1][1]이다.
좌표를 한 번 보면서 생각해보면 이해할 수 있을 것이다.
이러한 값을 구하기 위해서는 이 칸이 검은색이어야 하는지 하얀색이어야 하는지 판단할 수 있어야 한다.
이 방법은 간단하다. 먼저 가장 왼쪽 위에 해당하는 칸을 기준으로 정한다.
그리고 특정 칸이 기준이 되는 칸과의 (행 차이 + 열 차이)가 홀수면 색깔이 달라야하고 짝수면 색깔이 같아야한다.
<최종 코드>
import sys
def solution(c):
row_num=[0]*(n+1)
col_num=[0]*(m+1)
res=1e9
s=[[0]*(m+1) for _ in range(n+1)]
for i in range(1, n+1):
for j in range(1, m+1):
if ((i+j)%2==1 and chess[i-1][j-1]==c) or ((i+j)%2==0 and chess[i-1][j-1]!=c):
row_num[i]+=1
col_num[j]+=1
s[i][j]=1
s[i][j]=s[i-1][j-1]+row_num[i]+col_num[j]-s[i][j]
for i in range(1, n+1):
row_num[i]+=row_num[i-1]
for i in range(1, m+1):
col_num[i]+=col_num[i-1]
for i in range(k, n+1):
for j in range(k, m+1):
temp=s[i][j]-s[i-k][j]-s[i][j-k]+s[i-k][j-k]
res=min(res, temp)
return res
n, m, k =map(int, sys.stdin.readline().split())
chess=[list(sys.stdin.readline().strip('\n')) for _ in range(n)]
print(min(solution('B'), solution('W')))'백준 알고리즘' 카테고리의 다른 글
| [백준 3053][파이썬] 택시 기하학 (0) | 2023.02.13 |
|---|---|
| [백준 2231][파이썬] 분해 합 (0) | 2023.02.09 |
| [백준 9020][파이썬] 골드바흐의 추측 소수 판별 (에라토스테네스의 체) (0) | 2023.01.26 |
| [백준 2563][파이썬] 색종이. 이차원 배열 (0) | 2023.01.25 |
| [백준 10828][파이썬] 파이썬 스택 사용법 (0) | 2023.01.21 |