Network flow
다음과 같은 그래프가 있다고 하자. 각 에지의 가중치는 용량인데 용량은 흐를 수 있는 유량의 최대량이다.
네트워크 플로우 문제는 시작점 s에서 t까지 보낼 때 최대값을 가지는 플로우를 구하는 문제이다.

a/b라고 할 때 b는 유량의 총량인 용량을 의미하고 a는 현재 흐르는 유량을 의미한다.
당연히 a가 b보다 클 수는 없다.
다음 그림은 s에서 5만큼 t로 보낼 때의 예시이다.

최소 컷
컷이란 노드들을 두 개의 집합으로 분할하는 것이다.
시작점 s와 도착점 t는 서로 다른 집합에 있어야 한다.
아래는 두 집합 { s, a, c, d } 와 { b, t }로 나눈 예시이다.

다음과 같이 a->b, d->b, d->t 간선들이 컷에 속해있다.
해당 간선들의 비용 총합을 컷의 비용 총합이라고 하자.
s에서 t로 가는 유량의 총합은 컷의 비용 총합보다 클 수는 없다.
또한 컷은 위의 예시 뿐만 아니라 굉장히 많은 컷이 나올 수가 있는데 이러한 컷들의 비용 총합 중 가장 작은 값이 곧 최대 유량이 된다.
즉 네트워크 플로우의 최소 컷은 최대 유량이다.
포드 풀커슨 (Ford-Fulkerson) 알고리즘
우선 네트워크 플로우는 다음과 같은 3가지 조건을 만족시켜야 한다.
- 유량 보존의 법칙 : 출발지와 도착지를 제외하면 각 노드에서 들어오는 유량과 나가는 유량은 일치한다.
- 유량의 대칭성 : u에서 v로 3만큼 흐를 수 있다면 v에서 u로 -3만큼 흐를 수 있는 것이다.
- 용량 제한 : 간선의 유량은 간선의 용량보다 클 수는 없다.
포드 풀커슨의 핵심이 되는 부분이 2번이라고 볼 수 있다.
다음과 같은 그래프가 있다고 하면

다음과 같은 상황도 존재한다고 가정하는 것이다.

포드 풀커슨 알고리즘의 진행 과정을 파이썬 코드와 함께 보려고 한다.
def fordFulkerson(graph, s, t, n):- graph : 2차원 리스트. graph[a][b]는 a에서 b로 가는 간선의 총 용량
- s : 시작 노드
- t : 도착 노드
- n : 노드의 개수
노드의 번호는 0번에서 n-1번까지 있다고 가정한다.
먼저 더 흐를 수 있는 유량을 의미하는 remain 리스트를 초기화 한다. 당연히 처음에는 총량과 같다.
remain=[[0]*n for _ in range(n)]
for i in range(n):
for j in range(n):
remain[i][j]=graph[i][j]
max_flow=0 #최대 유량지금부터 반복을 시작한다. 더 이상 유량을 흘려보낼 수 있는 경로를 찾을 수 없을 때까지 반복한다.
while True:처음에는 bfs로 경로를 구한다.
#bfs 시작
####################################
visited=[False]*n
queue=deque()
queue.append(s)
visited[s]=True
path=[-1]*n #경로. 부모 노드를 저장. 거슬러 올라가면 경로 구할 수 있음
path[s]=-1 #처음 노드는 부모 노드가 없음
while queue:
a=queue.popleft()
for b in range(n):
if not visited[b] and remain[a][b]>0: #방문하지 않았고 갈 수 있다면
queue.append(b)
path[b]=a #부모 노드 저장
visited[b]=True
if not visited[t]: #목적지로 가는 경로가 없다면
break
#bfs 끝. 경로는 도착 노드인 t 부터 path를 보면서 부모 노드를 거슬러 올라가면 됨
#####################################path[b] = a의 의미는 s에서 t로 도달하는 경로 중 a 노드에서 b 노드로 가는 경로가 있다는 뜻이다.
path에는 부모 노드를 계속 저장하는데 이는 곧 경로를 의미한다.
다음과 같은 경로를 bfs로 찾았다고 하자.
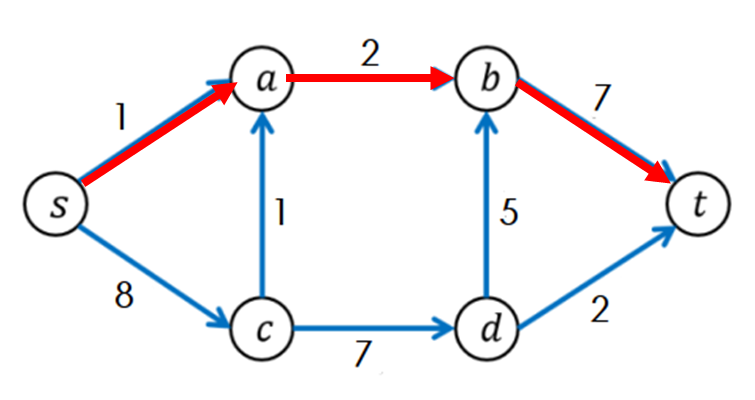
path[s]=a, path[a]=b, path[t]=b가 저장되어 있을 것이다.
이러면 t부터 거꾸로 거슬러 올라가면 t->b->a->s 경로를 알 수 있고 이를 뒤집은 경로가 bfs가 찾은 경로이다.
물론 연결만 되어있다면 모든 노드를 방문하기 때문에 c와 d에도 부모 노드가 저장되어 있겠지만 t부터 거꾸로 거슬러 올라가면 c와 d는 경로에 추가되지 않는다.
이제 하나의 경로를 구했다. 이 경로로 유량을 흘려보낼 것이다.
당연하게도 이 경로로 흘려보낼 수 있는 유량의 최대 크기는 간선들의 남아있는 용량 중 가장 작은 값이다.
다음과 같은 간선들의 남아있는 용량이 있다고 하면 가장 작은 값인 3보다 크게 보낼 수는 없을 것이다.

이제 경로를 통해 간선들의 남아있는 용량 중 가장 작은 값을 알아내야 한다.
b=t #경로를 거슬러 올라가기 위한 변수
min_remain=MAX #경로 간선들 중 가장 작은 용량을 구하기 위한 변수
while b!=s: #처음 노드에 도착할 때까지
a=path[b]
min_remain=min(min_remain, remain[a][b])
b=a경로를 거슬러 올라가면서 가장 작은 남아있는 용량을 알아낸다. 이제 이 용량만큼 유량을 흘려보내면 된다.
while b!=s:
a=path[b]
remain[a][b]-=min_remain
remain[b][a]+=min_remain
b=a
max_flow+=min_remain여기서 remain[a][b]-=min_remain을 통해 흘려보낸 유량만큼 남아있는 용량을 뺐다.
그런데 remain[b][a]+=min_remian은 무엇을 의미할까?
포드 풀커슨 알고리즘에서는 유량의 대칭성이 핵심이라고 했다.
a->b로 유량을 흘려보냈다면 b->a에 해당하는 경로가 없더라도 b->a로 유량을 흘려보낼 수도 있다.
이는 다음 그림을 통해 이해하는 편이 빠르다. 다음 그래프에서 s->c->a->b->t에 대한 경로를 먼저 찾았다고 하자.
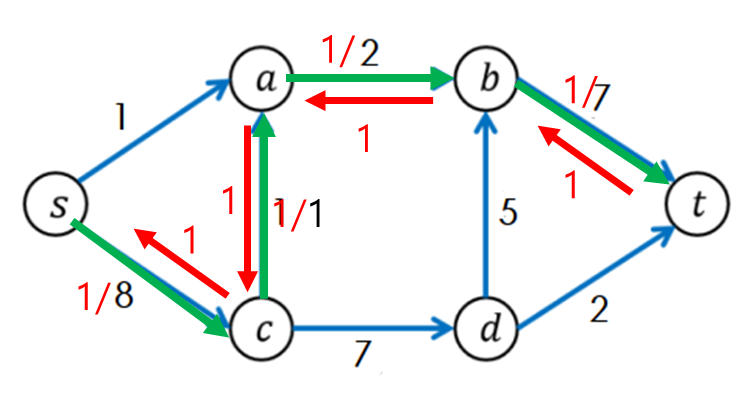
s->a->b->t에 해당하는 경로를 찾았다면 경로에 포함된 간선의 남은 용량들 중 가장 작은 값인 1만큼 흘려보내준다.
(remain[a][b]-=min_remain)
그리고 흘려보냈다면 거꾸로 올 수 있다는 것을 의미하도록 반대 방향에는 뺀 만큼 증가시킨다.
(remain[b][a]+=min_remian)
실제 해당 경로는 없지만 유량의 대칭성에 의해서 경로를 만들어주는 것이다.
이제 새로운 경로가 만들어졌다. 다시 한 번 bfs를 실시한다.
이번에는 새로 만들어진 경로를 통해서 가는 s->a->c->d->t에 해당하는 경로를 찾았다고 가정하자.
똑같은 과정을 반복한다. 역시나 새로운 경로가 생겼다.
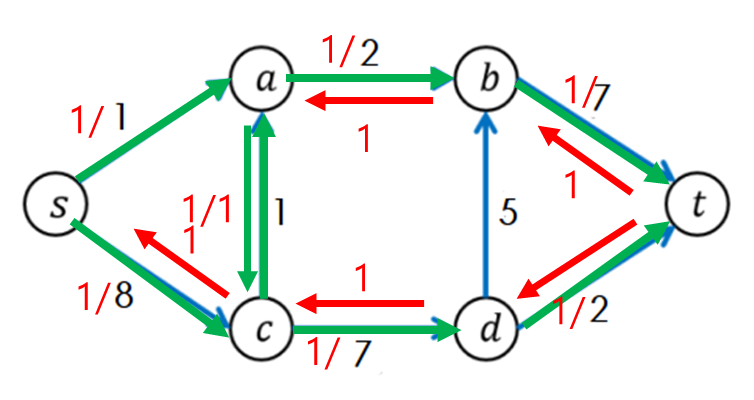
여기서 주의깊게 봐야할 부분은 a->c와 c->a이다.
원래는 c->a의 경로만 있었으나 c->a로 유량을 흘려보내면서 c->a의 용량이 꽉 차서 갈 수 없어지고 a->c의 새로운 경로가 생겨났다.
그런데 두 번째 반복에서 다시 a->c로 유량을 흘려보내면서 a->c의 용량이 꽉 차서 갈 수 없어지고 기존 경로인 c->a가 생겨났다.
즉 둘은 상쇄되었다고 보면 된다. 위 그래프가 복잡하므로 간단하게 표현하면 다음과 같다.
두 번째 반복이 끝났을 때의 흘려보낸 유량의 상황이다.
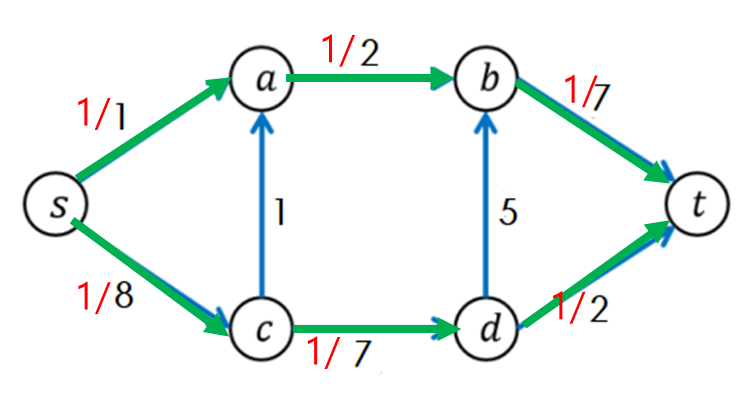
총 2만큼의 유량을 흘려보냈다.
보다싶이 s->c->a->b->t 경로로 유량을 1만큼 더 흘려보낼 수 있다. 이는 반복을 계속하면 될 것이다.
이렇게 반복하다보면 bfs를 끝냈음에도 t에 방문하지 않은 경우가 있을 것이다.
이것이 곧 더 이상 유량을 보낼 수 없는 상황에 도달했다는 것이고 그 때 반복문을 종료하면 된다.
참고로 포드 풀커슨이 제시한 방법을 bfs로 구현한 것이 에드몬드 카프 알고리즘이다.
<최종 코드>
import sys
from collections import deque
input=sys.stdin.readline
MAX=1e9
def fordFulkerson(graph, s, t, n):
#graph는 그래프. 간선의 비용 정보
#s는 시작 노드
#t는 도착 노드
#n은 노드의 개수
remain=[[0]*n for _ in range(n)]
for i in range(n):
for j in range(n):
remain[i][j]=graph[i][j]
max_flow=0 #최대 유량
while True:
#bfs 시작
####################################
visited=[False]*n
queue=deque()
queue.append(s)
visited[s]=True
path=[-1]*n #경로. 부모 노드를 저장. 거슬러 올라가면 경로 구할 수 있음
path[s]=-1 #처음 노드는 부모 노드가 없음
while queue:
a=queue.popleft()
for b in range(n):
if not visited[b] and remain[a][b]>0: #방문하지 않았고 갈 수 있다면
queue.append(b)
path[b]=a #부모 노드 저장
visited[b]=True
if not visited[t]: #목적지로 가는 경로가 없다면
break
#bfs 끝. 경로는 도착 노드인 t 부터 path를 보면서 부모 노드를 거슬러 올라가면 됨
#####################################
b=t #경로를 거슬러 올라가기 위한 변수
min_remain=MAX #경로 간선들 중 가장 작은 용량을 구하기 위한 변수
while b!=s: #처음 노드에 도착할 때까지
a=path[b]
min_remain=min(min_remain, remain[a][b])
b=a
b=t
while b!=s:
a=path[b]
remain[a][b]-=min_remain
remain[b][a]+=min_remain
b=a
max_flow+=min_remain
return max_flow'공부 > Algorithm' 카테고리의 다른 글
| [Algorithm] 플로이드 와샬(Floyd-Warshall) 알고리즘 (0) | 2023.06.23 |
|---|---|
| [Algorithm] 컨벡스 헐 만들기(Convex Hull), Graham Scan (0) | 2023.06.02 |
| [Algorithm][백준 11758][파이썬] CCW 알고리즘을 활용하여 선분의 교차 여부 판단 (0) | 2023.04.24 |
| [Algorithm] 펜윅 트리, 이진 인덱스 트리, BIT(Binary Indexed Tree)로 구간 합 문제 해결 (0) | 2023.04.23 |
| [Algorithm] RMQ (Range Minimum Query) (0) | 2023.04.19 |



댓글